Key Terms
- Natural numbers
- Whole numbers
- Integers
- Real numbers
- Real (number) line
- Coordinate
- Infinity
- Rational number
- Irrational number
- Interval notation
- Open interval
- Closed interval
- Half-open interval
- Infinite interval
- Absolute value
- Complex number
- Imaginary number
- Complex conjugate
Objectives
- Review the basic properties of the real numbers, as well as important subsets, particularly in relation to the real line
- Use interval notation to represent portions of the real line
- Define absolute value
- Study some basic characteristics of complex numbers
When we first learn to count, we are learning an ordered set of numbers: generally, the so-called natural numbers (1, 2, 3,...). As we gain a deeper understanding of numbers, we add the number 0, forming the whole numbers (0, 1, 2, 3,...). We can also add negative values of the natural numbers, expanding our view to integers (..., -3, -2, -1, 0, 1, 2, 3,...), and finally all the intermediate numbers between any two successive integers (decimal values). All of these numbers, including the integers and all possible numbers in between, are called the set of real numbers.
The Real Number Line
Just as with the natural numbers that we learn first as children, the real numbers are ordered, which we can intuitively define as the concept that given a pair of unique real numbers, one of them is greater than the other (and, conversely, one is less than the other). Thus, we can illustrate the real numbers using a number line--in this case, the real line or real number line. Every real number has a corresponding point on the line, and this line is generally drawn horizontally with the right-hand direction representing increasing value and the left-hand direction representing decreasing value. The real number corresponding to a particular point on the line is called a coordinate. Below is an illustration of the real number line. For obvious practical reasons, not all real numbers can be shown, so we generally show coordinates for a subset of the real numbers (often, integers, but different situations call for different subsets). A coordinate point is shown for the number 1.5.
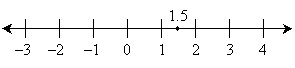
Think of any number; regardless of the number, you can always think of a number that is greater than or less than the one you chose. Thus, we say that the real number line extends to infinity in both the positive and negative directions. What is illustrated above is a portion of the real line. Note carefully, however, that infinity (typically written as ∞) is not a real number--it simply represents the fact that the real line extends indefinitely. In the positive (right) direction, the real line extends toward +∞ (positive infinity); in the negative (left) direction, it extends toward –∞ (negative infinity).
We can further divide the real numbers into two distinct classes: rational numbers and irrational numbers. A rational number is any real number that can be expressed exactly as a fraction whose numerator is an integer and whose denominator is a non-zero integer. That is, a rational number is a fraction ![]() where a is an integer and b is an integer other than zero. In decimal form, a rational number is either a terminating decimal (such as 2, 1.375, and –0.5) or a repeating decimal (such as 0.3333...). An irrational number, on the other hand, cannot be written as a fraction with an integer numerator and denominator. Irrational numbers in decimal form are nonrepeating, nonterminating decimals. Examples of irrational numbers include
where a is an integer and b is an integer other than zero. In decimal form, a rational number is either a terminating decimal (such as 2, 1.375, and –0.5) or a repeating decimal (such as 0.3333...). An irrational number, on the other hand, cannot be written as a fraction with an integer numerator and denominator. Irrational numbers in decimal form are nonrepeating, nonterminating decimals. Examples of irrational numbers include ![]() and π. Rational numbers and irrational numbers are mutually exclusive: they have no numbers in common. Furthermore, they span the entire set of real numbers; that is, if you add the set of rational numbers to the set of irrational numbers, you get the entire set of real numbers. Each of these sets has an infinite number of members.
and π. Rational numbers and irrational numbers are mutually exclusive: they have no numbers in common. Furthermore, they span the entire set of real numbers; that is, if you add the set of rational numbers to the set of irrational numbers, you get the entire set of real numbers. Each of these sets has an infinite number of members.
Practice Problem: Draw the real line and add points for the coordinates –1, 2, and π.
Solution: A relevant portion of the real line is shown below. The coordinates for the listed points are shown above the line for clarity only.
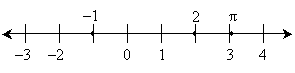
Practice Problem: Determine which of the following are rational numbers and which are irrational: 0, 1, π, ![]() , 0.11111...,
, 0.11111..., ![]() .
.
Solution: A rational number is any real number that can be written as a fraction whose numerator and denominator are integers (in decimal form, this means a number that is either a terminating or repeating decimal). Thus, 0, 1, 0.11111..., and ![]() are rational. The numbers π and
are rational. The numbers π and ![]() are irrational because they cannot be expressed exactly as fractions involving integers only.
are irrational because they cannot be expressed exactly as fractions involving integers only.
Interval Notation
Because we can't list every single real number between, say, 1 and 2, we need some way to identify continuous portions of the real number line. To that end, we can use interval notation. An interval has two endpoints that define the smallest number and largest number in that interval--we'll call these numbers a and b for generality. An open interval (a, b) is the set of all real numbers x such that a < x < b. A closed interval [a, b] is the set of all real numbers x such that a ≤ x ≤ b. (In other words, an open interval is the set of all real numbers between a and b excluding a and b, and a closed interval is the set of all real numbers between a and b including a and b.) We might also refer to half-open intervals (a, b], where a < x ≤ b, and [a, b), where a ≤ x < b. An infinite interval is an interval extending to either +∞ or –∞: note that because ∞ is not a real number, however, we always use "open" notation for that portion of the interval. Thus, (–∞, a] is all x such that –∞ < x ≤ a, and (b, ∞) is all x such that b < x <∞.
Practice Problem: Write interval notation for each of the following sets of real numbers x.
a. –2 < x < 0 b. x ≥ 0 c. 3 ≤ x ≤ 4 d. –∞ < x < ∞
Solution: In each case, use parentheses when < or > is used and use brackets when ≤ or ≥ is used. Write the intervals according to the convention described above.
a. (–2, 0) b. [0, ∞) c. [3, 4] d. (–∞, ∞)
Absolute Value
A useful tool in examining real numbers is absolute value, which can essentially be defined as the value of a number without regard to sign. Mathematically, the absolute value of a number c, which is written as |c|, is the following:
![]()
For example, |-3| = |3| = 3. Another way to define absolute value for a real number c is as follows:
![]()
Complex Numbers
We will not spend much time on the details of complex numbers, as they could easily constitute a number of university-level courses, but they do crop up in calculus regularly, and it behooves us to recognize them and have some facility with them. Complex numbers are distinguished from real numbers by the presence of the value i, which is defined as ![]() . In other words, i2 = –1. But no real number, when squared, is ever equal to a negative number--hence, we call i an imaginary number. In general, a complex number has the form a + bi, where a and b are real numbers. (a is called the real part and b is called the imaginary part.) Because i is not a real number, complex numbers cannot generally be placed on the real line (except when b is equal to zero). Complex numbers must be treated in many ways like binomials; below are the rules for basic math (addition and multiplication) using complex numbers. Note that a, b, c, and d are assumed to be real.
. In other words, i2 = –1. But no real number, when squared, is ever equal to a negative number--hence, we call i an imaginary number. In general, a complex number has the form a + bi, where a and b are real numbers. (a is called the real part and b is called the imaginary part.) Because i is not a real number, complex numbers cannot generally be placed on the real line (except when b is equal to zero). Complex numbers must be treated in many ways like binomials; below are the rules for basic math (addition and multiplication) using complex numbers. Note that a, b, c, and d are assumed to be real.
(a + bi) + (c + di) = (a + c) + (b + d)i
(a + bi) (c + di) = (ac – bd) + (bc + ad)i
The complex conjugate of a complex number a + bi is simply a – bi. Complex conjugates have the interesting (and useful) characteristic that their product is a real number:
(a + bi) (a – bi) = a2 + abi – abi – (bi)2 = a2 – (b2i2) = a2 – (b2)(–1) = a2 + b2
Practice Problem: Calculate the result in each case.
a. (3 + 4i) – (2 – i)
b. (5 + i) (3 – i)
c. Complex conjugate of 2 – 10i
Solution:
Use the basic rules of math and the properties of complex numbers described above. Note carefully that i2 = –1.
a. 1 + 5i b. 16 – 2i c. 2 + 10i






















