Key Terms
Objectives
Introduction to Limits
Consider the simple parabola ![]() below:
below:
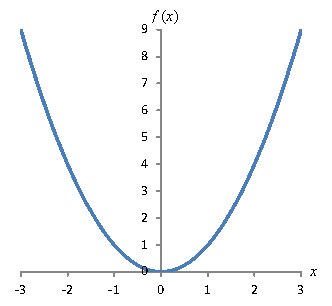
If you keep following the curve as x gets larger and larger, you find that it also gets larger at an increasing rate. You could (quite correctly) say that the function f is unlimited as x increases--or, alternatively, f has no limit as x increases.
Now, consider another example: ![]() .
.
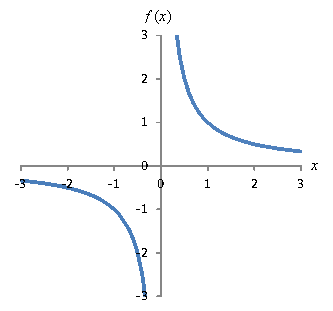
As x gets very large in this case, the function f approaches 0. For instance,
![]()
![]()
![]()
![]()
and so on. Although no value of x is large enough to make f equal to zero, f gets arbitrarily close to zero as x approaches infinity (∞). Mathematically, we say that the limit of f(x) as x approaches ∞ is 0. Or, symbolically,
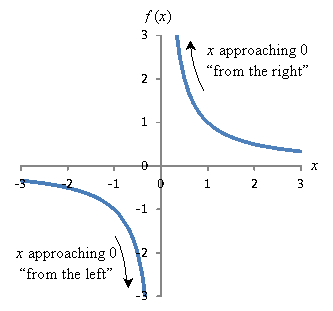
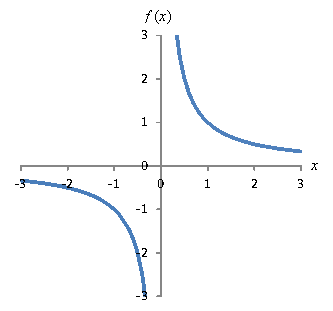
Likewise, if x approaches -∞, the function f in this case also gets arbitrarily close to zero. But we need not restrict limits to extreme values of the independent variable. What about other interesting features of this function? Let's consider how to deal with the limits as we approach x = 0. First, note that the limit depends on the direction from which the x value is approached. In this case, if we start on the left side and approach x = 0, the function f gets smaller and smaller (in the sense of a larger magnitude but with a negative sign) without limit. To represent this situation symbolically, we call the limit -∞, but this simply means that the function has no minimum real value. We use a small "–" superscript to indicate approach from the left: When we approach x = 0 from the right (indicated by a "+" superscript), f gets arbitrarily large, so we say the limit is ∞. We can also look at the limit of any arbitrary point--not just "special" points. Consider x = 1. So, let's look once more at the general expression for a limit on a given function f(x) as x approaches some constant c. Considering all the examples above, we can now say that if a function f gets arbitrarily close to (but not necessarily reaches) some value L as x approaches c from either side, then L is the limit of that function for x approaching c. In this case, we say the limit exists. One-sided limits are when the function approaches a particular value from only one side (as in the function below). In this case, the limit Often we can determine the limit by simply calculating f(c), but clearly this doesn't always work (particularly if c is not in the domain of f). Also, we may need to consider the direction from which we're approaching c (for one-sided limits). Usually, however, you can easily calculate a limit if you also look at a graph or table of values around x = c. Practice Problem: Calculate the following limits. a. Solution: It helps to first graph the function to see these limits.
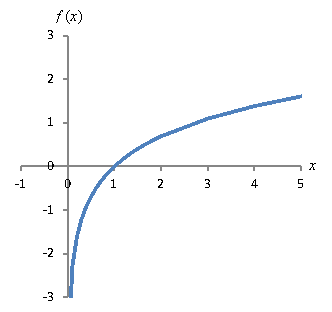
a. For this limit, consider the value of ln x as x gets closer and closer to 0. The function approaches -∞, so the limit is b. In this case, we can simply plug c into the function. Note that the limit is 0 regardless of the direction of approach. c. Here, as x gets arbitrarily large, so does ln x (i.e., the function has no real maximum value). Thus, d. Again in this case, the direction of approach doesn't matter. We can simply plug e into the function. Rules of Limits Some limits may involve complicated expressions. In these and other cases, it is often helpful to use rules that simplify calculations. Below are the basic properties of limits for arbitrary functions f(x) and g(x) and arbitrary constant k. These rules for limits enable us to break complicated expressions into simpler ones for the purposes of finding a limit. Practice Problem: Describe in words why for polynomial p(x), the following is always true. Solution: Recall that a polynomial p(x) has the following form, where the values ci (where i = 0, 1, 2, 3,., n) are constants: As x approaches k, the polynomial (whatever its form) approaches p(k) because the domain of a polynomial is all real numbers. Thus, when we are dealing with limits for polynomials, we can simply substitute the limiting value for x directly into the function. The mathematical proof for this fact is not overly complicated, but the result is fairly intuitive. Practice Problem: Calculate the following limits. a. Solution: In each case, you can use a number of approaches. One is to graph the function and look at the behavior of the function near the limiting x value (this is often helpful regardless of the approach you take). Alternatively, you can use the rules of limits and, where appropriate, simply substitute. a. Here, substitution is possible without any problem. You can also use the rules of limits. b. In this case, the function is a polynomial of degree 2. We can simply substitute. c. For this function, you cannot directly apply the rules of limits and substitution. Look at the graph-note particularly that the x value is being approached from the right. Application of Limits: Continuity
Intuitively, we can say that the function is continuous (i.e., it has no "breaks" in it) on the left side of x = 0 and on the right side of x = 0, but not at x = 0. But what about a more mathematical definition? We can use limits. A function is continuous at a particular point x = c if the following conditions are all satisfied: Note that a function is continuous on an open interval (a, b) if it is continuous at all points in that interval. Practice Problem: Determine if the function is continuous at the given point. a. Solution: For problem a, note that the function is equal to the line x + 2, except that it is missing the point (1, 3). Interestingly, the limit does exist here: The function is not defined at x = 1, however. Therefore, we cannot use substitution to find the limit. Because the function violates one (it actually violates two) of the conditions for continuity, it is not continuous at x = 1. For part b, note that none of the conditions for continuity are satisfied. The limit does not exist (it is ∞), and the function is not defined at x = 0. Therefore, the function is not continuous at x = 0. For part c, note that the function is defined at x = e: ln e = 1 Furthermore, the limit is defined and can be calculated by substitution: Thus, ln x is continuous at x = e. ![]()
![]()
![]()
![]()
![]()
![]()
![]() does not exist; we can find the one-sided limits, however, as we did above.
does not exist; we can find the one-sided limits, however, as we did above.![]() b.
b. ![]() c.
c. ![]() d.
d. ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
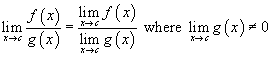
![]()
![]()
![]()
![]() b.
b. ![]() c.
c. ![]()
![]()
![]()
![]()
![]() .
.
![]() exists
exists
![]()
![]() at x = 1 b.
at x = 1 b. ![]() at x = 0 c. ln x at x = e
at x = 0 c. ln x at x = e![]()
![]()























