• Polynomial
• Degree
• Linear function
• Slopey-intercept
• x-intercept
• Root
• Zero (of a function)Quadratic function
• Quadratic formula Rational function

Objectives

• Identify polynomials and their basic characteristics
• Define rational functions
• Find the domain, range, and roots of simple polynomials and rational functions

 

Introduction to Polynomials

 

Polynomials are a type of function that you will see regularly as you study mathematics. A polynomial is a series of terms, each of which is the product of a constant coefficient and an integer power of the independent variable. A general polynomial function f in terms of the variable x is expressed below.

 

 

Here, the coefficients c_i are constant, and n is the degree of the polynomial (n must be an integer where 0 ≤ n < ∞). Note that a line, which has the form (or, perhaps more familiarly, y = mx + b), is a polynomial of degree one--or a first-degree polynomial. A quadratic function, , is a second-degree polynomial.

 

Linear Functions

 

Linear functions (apart from constant, or zeroth-degree functions) are the simplest kind of polynomial. Given the form , the slope of the line is c₁ and the y-intercept is c₀. Here, the slope is defined as the change in the value of f (or Δf) divided by a corresponding change in x (or Δx), and the y-intercept is the value of f at x = 0. These characteristics are illustrated graphically below for the function .

 

 

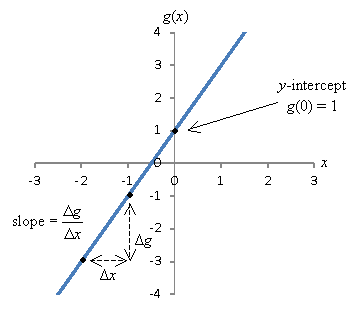
In general, many functions have y-intercepts--again, for a function f(x), this is simply f(0). (Not all functions have a y-intercept however, as not all are defined at x = 0. For instance, the function is not defined at x = 0, so it has no y-intercept.) Because a function must pass the vertical line test as we noted previously, a function can have at most one y-intercept.

 

Some functions may also have x-intercepts: for a function g(x), these are values of x for which g(x) = 0. In other words, an x-intercept is a solution to the equation g(x) = 0. The values of x that satisfy this equation are also called roots or zeroes of the function. A function may have many, one, or no roots. In our linear example above, the function has a root at , since

 

 

The root of this function is illustrated graphically below.

 

 

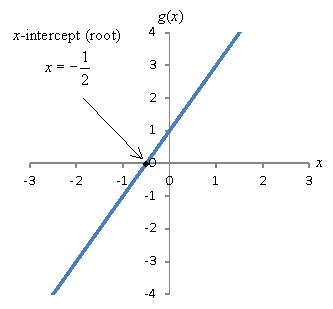
Quadratic Functions

 

You may also be familiar with quadratic functions (second-degree polynomials), which have the form . Quadratic functions, like all polynomials, have a y-intercept c₀. They can have none, one, or two roots, which can be determined using the quadratic formula, which is expressed below.

 

 

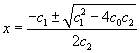
Note that a first-degree polynomial (linear function) can only have a maximum of one root. The pattern holds for all polynomials: a polynomial of root n can have a maximum of n roots.

 

 

Practice Problem: Find the roots, if they exist, of the function .

 

Solution: You can use a number of different solution methods. One is to evaluate the quadratic formula:

 

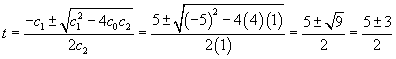
t = 1, 4

 

Alternatively, you can factor to find the values of x that make the function h equal to zero.

 

t = 1, 4

 

You can also graph the function to find the location of roots--but be sure to test your answers in the equation, as graphs are not exact solution methods generally. The graph for h(t) is shown below with the roots marked with points.

 

 

 

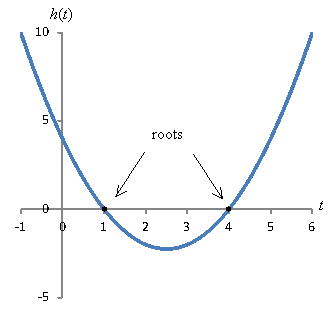
Finding the roots of higher-degree polynomials is a more complicated task.

 

Introduction to Rational Functions

 

Rational functions are fractions involving polynomials. A rational function f(x) has the general form shown below, where p(x) and q(x) are polynomials of any degree (with the caveat that q(x) ≠ 0, since that would result in an #ff0000 function).

 

 

Note that all polynomials are rational functions (a polynomial is a rational function for which q(x) = 1), but not all rational functions are polynomials. An example of a rational function is the following.

 

 

A note of caution: although you can simplify the expression above, the result may not be identical to the original function. To illustrate this point, let's factor the numerator of g(r).

 

 

Naturally, the temptation is to cancel one factor of r – 1 from both the numerator and the denominator, leaving the expression below:

 

 

Thus, we see that g(r) is linear. And if we graph the first expression (with the polynomial denominator), the result will be the line r – 1 except that r cannot equal 1, since r = 1 is not in the domain of g(r). In the graph, this strange result appears as a "hole," as illustrated below using an open circle at r = 1. Thus, we must treat rational functions carefully with regard to changing the expression.

 

 

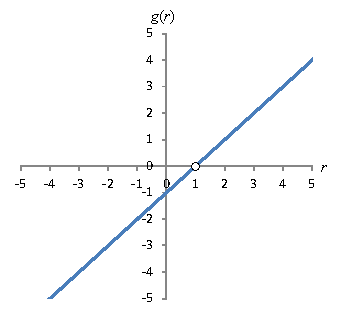
Practice Problem: Find the domain and range of the function , and graph the function.

 

Solution: The domain of a polynomial is the entire set of real numbers. The limiting factor on the domain for a rational function is the denominator, which cannot be equal to zero. The values not included in the domain of t(x) are the roots of the polynomial in the denominator. Let's factor both the numerator and denominator.

 

We can see from this factoring that the domain of t(x) is all real numbers except x = –1. That is, the domain includes the intervals (-∞,-1) and (-1, ∞). To find the range, let's plot the graph of the function. To do so, we can simplify it by eliminating like factors:

 

 

 

 

Since the limitation that x cannot be –1 remains after simplification, we can plot the simplified function without worrying about neglecting holes in the graph.

 

 

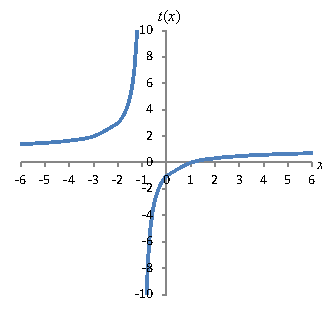
Note that the x can never be –1 because the function goes to infinity (or negative infinity) as it approaches this value. Also note that the range of the function includes all real values except t = 1. It gets very close to t = 1, but it never reaches this value (the numerator is never equal to the denominator!).