How to Use Inverse Trigonometric Functions to Solve Problems

Key Terms

Identity

Odd function

Antisymmetric

Even function

Symmetric

Objectives

Investigate simple trigonometric identities

Use inverse trigonometric functions to solve simple problems

In this article, we will look more carefully at some of the algebraic properties of trig functions.

Trigonometric Identities

Trig functions are closely related, and it is often helpful to express them in different forms. To this end, identities are often useful. A trig identity is an equation of two expressions that always holds. A very simple trig identity is the following:

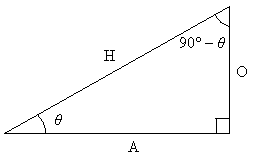
We can derive this identity by looking at a right triangle with acute angle θ.

We should already know that , , and .

Then note that:

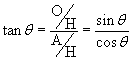
Want to learn more? Take an online course in Precalculus.

The following practice problem illustrates the proof for another common trig identity: the Pythagorean identity. First, however, note below the commonly used manner of writing exponents of trig functions:

Practice Problem: Prove the identity .

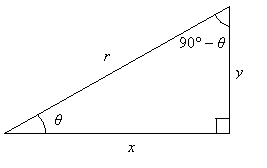
Solution: We can once again use a right triangle to prove that this identity holds generally, although we use slightly different notation for variety.

Now, replace each trig function with the associated side measures for the right triangle above.

But note that by the Pythagorean theorem, x² + y² = r². Thus,

For this reason, this identity is often called the Pythagorean identity.

A couple other common trig identities are listed below.

Other Relationships Among Trigonometric Functions

By looking again at a right triangle, we can also note some other important relationships among trig functions.

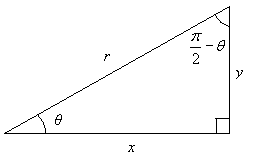
We can write the following expressions on the basis of the above diagram.

Thus,

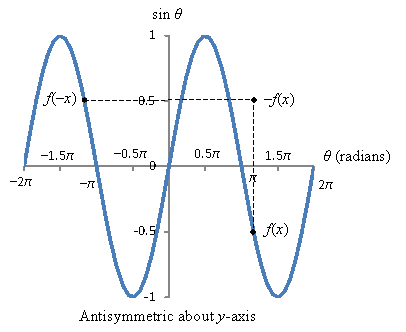
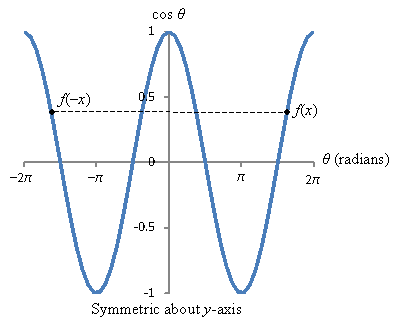
Graphically, we can also see these relationships. First, note that the sine function is an odd function. In general, any function f(x) is an odd function if . Another way of looking at this is that the function f(x) is antisymmetric about the y-axis. In addition, note that the cosine function is an even function. Any function f(x) is an even function if ; this means the function is symmetric about the y-axis.

Now, note that for sin θ, if we subtract from the argument (θ), we get the negative cosine function. (Subtracting from the argument of sin θ has the effect of shifting the function to the right by .)

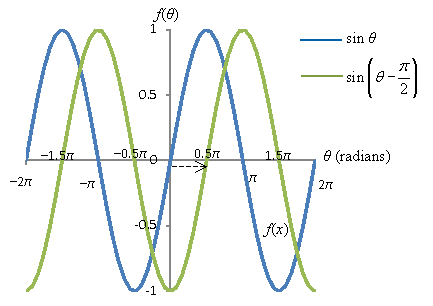
But using the antisymmetry of the sine function, we can derive the previous form of the identity:

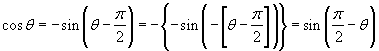
The same kind of graphical reasoning can be used to prove the other identity. Below are several other useful trigonometric identities.

Inverse Trigonometric Functions

The final set of additional trigonometric functions we will introduce are the inverse trig functions. These are sometimes written using a superscripted –1 (as we have done previously for generic inverse functions), or they use the prefix arc. Thus, for instance, arcsin θ and sin^-1 θ are the same function. Again, following the same pattern as our previous inverse functions, note the following relations.

Because trigonometric functions are not one-to-one, however, these inverses must be treated carefully (by limiting their ranges such that they do not violate the vertical line test and thus remain functions). We will not deal at length with the graphical versions of these functions. Note, however, that the domain of the inverse trig functions is the same as the range of the corresponding standard trig function. Thus, for instance, the domain of arcsin θ is [–1, 1], because the range of sin θ is [–1, 1].

Let's now look at a simple example of the application of inverse trig functions.

What's the value of this expression? First, note that the inverse sine is simply an angle.

Take the sine of both sides and apply the above-mentioned rules.

The question is then which values of θ satisfy the equation sin θ = 1. One approach is to simply look at the graph of the sine function.

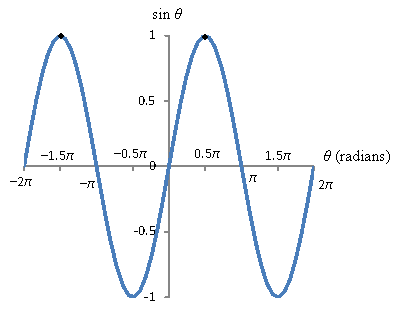
Note that if we extended the sine function to infinity in either direction, we'd end up with an infinite number of solutions θ. There solutions are the following:

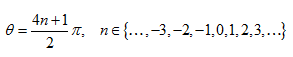
The notation here simply means that n is any element of () the set of integers. (Another way to write this is , where is the set of integers.)

You may find this result problematic. Which answer should you select in a particular problem? As it turns out, the parameters of the problem will often determine which solution is acceptable. For instance, if you need to calculate an inverse trig function to calculate an interior angle of a triangle, you can immediately discard all negative solutions as well as any solution greater than or equal to π. In more-complicated problems, however, a number of solutions may be correct. Again, this will depend on the details of the problem.

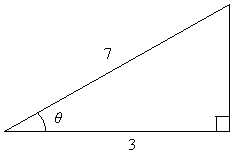
For cases where you cannot find a clean solution (as in the case where sin θ = 1), you may need to use a calculator. Most scientific calculators include inverse trig functions; just remember to appropriately set your calculator for radian or degree mode, depending on which angle system you're using. Your calculator will return one solution (basically, either in the range or [–π, π]). Other solutions may apply, however--you can look at the graphs of the functions to determine these solutions.

Practice Problem: Find the angle θ for the figure below.

Solution: We can use right-triangle trig here, but we must apply inverse trig functions. Note the following relationship.

Apply the inverse cosine function to both sides.

Use a calculator in radian mode:

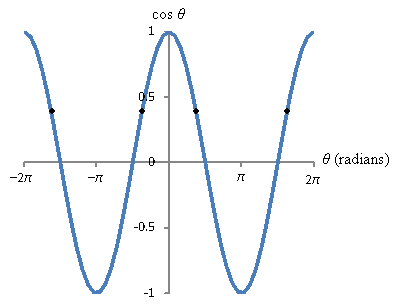
This angle is also approximately 64.6°, which is sensible for this triangle. Let's look at the graph of the cosine function. The other possible values for θ are illustrated as points on the curve. Because we are dealing with a triangle, we discard all negative values as well as any values greater than or equal to π. That leaves just one possible value for θ, which is our solution above.