Exponential Functions

 

 

You should already be familiar with exponents. By way of review, however, here are the basic rules of math involving exponents. Note first that in the expression a^b, a is the base and b is the exponent. The rules below are expressed in terms of the base e, which is a special irrational number with a variety of applications in math and science. The number e is approximately equal to 2.71828. These rules apply to any base, however.

 

 

 

 

Let's now look at the simple exponential function , which is plotted below.

 

 

 

 

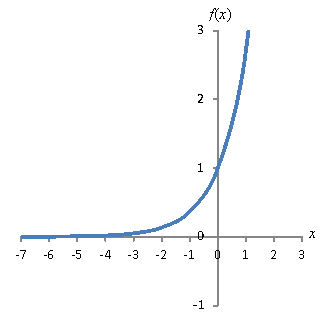
This function has a domain (-∞, ∞) and a range (0, ∞). It also has an asymptote at y = 0 (the x-axis); note that 0 is not in the range of the function. Furthermore, it intercepts the y-axis at f(0) = 1 (since any number raised to the zeroth power is 1), but it has no real roots.

 

 

This function has application, for instance, in the case of interest on investments. Given a principle investment P and a continuously compounded interest rate r, the total value V of the investment at time t (where t and r are both expressed in terms of the same unit of time) is

 

 

 

 

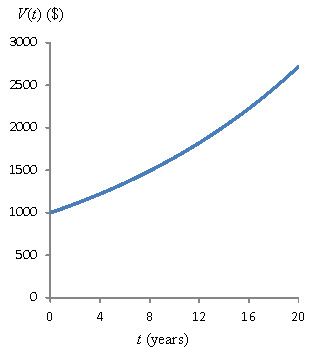
Note in this case that the y-intercept (value at t = 0) is V(0) = P, or the initial investment amount. The value of the investment grows at an increasing rate as time goes on (hence the fact that a small interest rate can greatly increase value in a fairly short amount of time). Below is a plot of the value V(t) of a $1,000 investment with an annual interest rate of 5%. Here, t is measured in years. The function is . After 20 years, even at just 5% interest, the initial investment has nearly tripled.

 

 

 

 

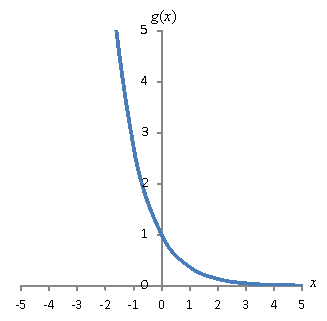
Also noteworthy is the exponential function , which is plotted below. Note that unlike , where the function increases as x increases, the function decreases as x increases. Functions similar to this one are useful for modeling physical phenomenon that involve decay over time, such as the decreasing amplitude of a spring in motion as friction works on it. The function has the same domain and range as .

 

 

 

 

Logarithmic Functions

 

 

A logarithm is the inverse function of exponentiation. Let's say we have a function . By our definition of inverse functions, a logarithmic function g(x) (the inverse of f(x)) would satisfy the following expression.

 

 

 

 

Generally, the simple logarithmic function has the following form, where a is the base of the logarithm (corresponding, not coincidentally, to the base of the exponential function).

 

 

 

 

When the base a is equal to e, the logarithm has a special name: the natural logarithm, which we write as ln x. This natural logarithmic function is the inverse of the exponential . Thus,

 

 

 

 

This means that the following two equations must both be true.

 

 

 

 

Below are the basic rules of logarithms. These are expressed generally using the arbitrary base a, but they apply when a = e and the logarithm is expressed as ln (which is identical to log_e).

 

 

 

 

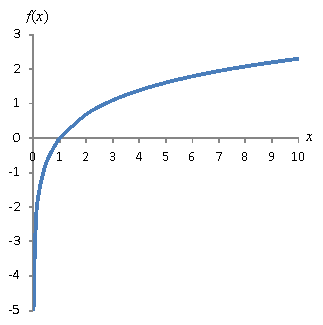
Below is a graph of the natural logarithm function. Note that because the exponential is always positive for real values of x, the domain of the function ln x is (0, ∞). A vertical asymptote exists at x = 0. The range of the function is (-∞, ∞). You might also notice that the graph of the function ln x looks like the graph of the function rotated clockwise 90° and then rotated 180° around the vertical axis. This is a general characteristic of inverse functions.

 

 

 

 

 

Practice Problem: How long does it take for an initial investment of $100 to double, given an annual interest rate of 10% that is compounded continuously?

 

 

Solution: We can use the rules of exponents and logarithms to solve this problem. Recall from above that , where P is the initial investment (principal), r is the interest rate, and V is the value of the investment at time t (expressed in years). When $100 has doubled, it is $200:

 

 

 

 

 

We can apply natural logarithms to solve this problem. Take the natural logarithm of both sides and apply the rules of logarithms (we drop the dollar signs for simplicity):

 

 

 

 

 

 

 

 

 

 

Thus, at a continuously compounded annual interest rate of 10%, an investment doubles roughly every seven years.

 

 

 

Practice Problem: Solve the equation below for the variable c.

 

 

 

 

Solution: Here, we can apply the rule of inverse functions:

 

 

 

 

Thus, apply the exponential function to both sides of the given equation, then evaluate each side.

 

 

 

 

 

 

Now, check the result by plugging it back into the original equation.