Key Terms
o Triangle
o Vertex
o Equilateral triangle
o Scalene triangle
o Acute triangle
o Obtuse triangle
o Right triangle
o Pythagorean theorem
o Hypotenuse
o Leg
o Altitude
o Base
Objectives
o Identify various types of triangles
o Know how to use the Pythagorean theorem to find the lengths of sides for right triangles
o Identify the altitude(s) and base(s) of a triangle
o Calculate the area of a triangle
A triangle is aptly named: it is composed of three (tri) angles formed by three non-coincident, non-parallel lines. That the lines are non-coincident means they do not overlap, and that they are non-parallel means that each line intersects with every other line. Correspondingly, a triangle also has three sides. Try drawing any three non-coincident, non-intersecting lines; if you extend them far enough, they will all intersect and form a triangle, such as the one shown below.
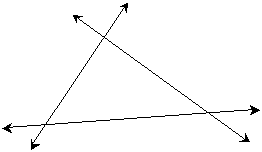
Of course, three intersecting line segments are sufficient to form a triangle as well; in either case, the intersection points may or may not be indicated with labeled (or unlabeled) points. These intersection points are called vertices (which is the plural form of vertex).
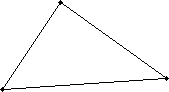

Using what we have learned about geometry so far, we can prove a well-known property of triangles: the sum of the measures of the angles in a triangle is 180°. Let's start with an arbitrary triangle ABC, which is shown below. Note that the figure is not necessarily drawn to scale.
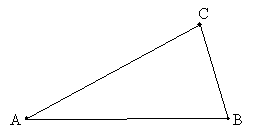

Now, extend line segment AB (which we can write as ![]() ), forming line p, and add a line q that is parallel to p and that intersects point C. We now use the vertex labels as angle labels (in italics) to avoid cluttering the diagram.
), forming line p, and add a line q that is parallel to p and that intersects point C. We now use the vertex labels as angle labels (in italics) to avoid cluttering the diagram.
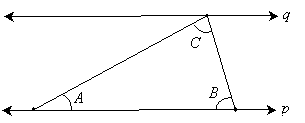

Note that the two line segments are simply transversals: they intersect two parallel lines. We can therefore use the properties concerning parallel lines cut by transversals to make inferences about the angles shown in the diagram. By the rules of corresponding angles, we can infer the following:
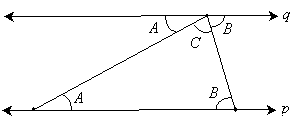

But notice that the three angles A, B, and C formed with the line q are supplementary angles. (Although we learned about supplementary angles in the context of only two angles, the same principle also applies to three or more angles as well.) Thus,
A + B + C = 180°
As a result, we have proven that the sum of the angles in a triangle is 180°. Note that we made no assumptions about any of the angles, nor was our drawing assumed to be to scale. This result is general and applies to all triangles.
Practice Problem: What is the measure of angle a below?
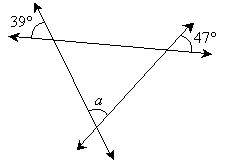
Solution: The three lines in the diagram form a triangle. Because vertical (opposite) angles are equal in measure, we can add the following information to the diagram.
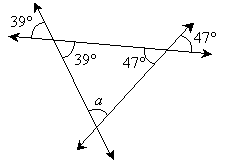
Finally, because the angles of a triangle sum to 180°,
39° + 47° + a = 180°
a = 180° – 39° – 47° = 94°
Thus, the measure of angle a is 94°.
Types of Triangles
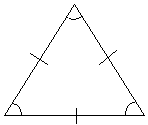
It is helpful to point out several classes of triangles with unique properties that can aid geometric analysis. One particular type of triangle is an equilateral triangle; the defining property of this triangle is that all its sides are of equal length. In addition, its angles are likewise equivalent. An equilateral triangle is shown below; note that sides of equal length are marked with the same slash symbol.
Another type of triangle is an isosceles triangle, which has two sides of equal length. (Unless an isosceles triangle is defined as having exactly two sides of equal length, an equilateral triangle is also an isosceles triangle--but not vice versa.) The two angles adjacent to the third (unequal) side are also equal. An isosceles triangle is shown below. (Different angle measures are denoted using different marks, as with different side lengths.)
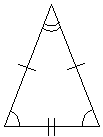
A scalene triangle has three sides of different lengths. In addition, if all three angles in a triangle are less than 90°, then that triangle is accordingly called an acute triangle. If an angle is greater than 90°, then the triangle is called obtuse. (Note that only one angle in a triangle can be grater than 90°, since the sum of all the angles is only 180°.) If a triangle has an angle of 90°, then it is called a right triangle. Right triangles have various special properties, one of which is that the lengths of the sides are related by way of the Pythagorean theorem. Consider a right triangle such as that shown below.
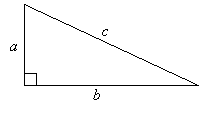
The side c, which is opposite the right angle, is called the hypotenuse. The other two sides are called legs. We can relate the lengths of the sides by way of the following formula (the Pythagorean theorem):
![]()
This theorem only applies to right triangles. If we know the lengths of two of the sides for a right triangle, we can calculate the length of the third side.
Practice Problem: How many degrees are in each angle of an equilateral triangle?
Solution: Recall from the definition that the angles of an equilateral triangle all have equal measures. Let's call this measure α. Combine this with the fact that the sum of all the angles in a triangle is 180°; we can then write
![]()
![]()
Thus, each angle in an equilateral triangle has a measure of 60°.
Practice Problem: Find the length of the unknown side in the triangle below.


Solution: Because this triangle is a right triangle, we can use the Pythagorean theorem. The unknown side is a leg, which we can call x, and the side of length 5 is the hypotenuse. Then,
![]()
![]()
![]()
Thus, the unknown side has a length of 4 (technically, the length is "4 units," but the units are unspecified and therefore are occasionally unmentioned). Note that we use the positive square root in the calculation above; a negative result would not have any meaning in this context.
Other Aspects of Triangles
When analyzing triangles, it is sometimes helpful to identify the altitude of a triangle. The altitude is a line segment that passes through a vertex and that is perpendicular to the side opposite that vertex. This opposite side, in this case, is called the base of the triangle. An altitude is shown as a dashed line in the triangle below.

In some instances, we may want to calculate the area of a triangle. You may already well know that the area of a rectangle is simply the product of its length and its width (![]() ), but the area of a triangle may seem less clear. We can, however, relate the triangle to a rectangle as follows. Let's use the generic triangle diagram above, and let's make a copy of the triangle, as shown below. We also define several lengths in the triangle.
), but the area of a triangle may seem less clear. We can, however, relate the triangle to a rectangle as follows. Let's use the generic triangle diagram above, and let's make a copy of the triangle, as shown below. We also define several lengths in the triangle.
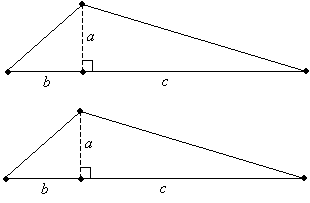
Now, we can cut the second triangle in half along the dashed altitude line and then combine like pieces.
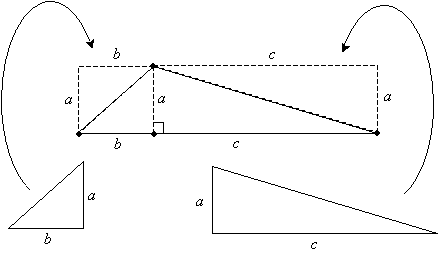
Notice that now we have formed a rectangle with a length of b + c (which is the length of the base of the triangle) and a width of a (which is the altitude, or height, of the triangle). But we know that the area of a rectangle is simply the length times the width. In this case, we combined two equivalent triangles to form the rectangle. Thus, the area of one of the triangles is half the area of the rectangle. We have therefore shown that the area of a triangle is one-half the product of the lengths of the base and altitude (or height). If the length of the base is B (which, above, is b + c) and the height is H, then the area A is
![]()
Although we used a particular triangle as shown above, the same process can be repeated for any triangle; the principles are the same even though the particular example might differ. In addition, you can choose any of the three altitude-base combinations in a triangle; the area calculation will lead to the same result in each case.
Practice Problem: Find the area of the triangle below.
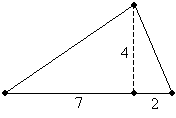
Solution: The area of a triangle is half of the product of the base and height (or altitude). In the diagram, the triangle is shown with a height of 4 units and a base of 7 + 2 = 9 units. The area is thus
![]()
The triangle has an area of 18 square units.























