Understanding Variable Use in Algebra

Key Terms

o Variable

o Algebraic relation

o Independent variable

o Dependent variable

o Equation

Objectives

o Understand what a variable is

o Differentiate between a dependent and independent variable

o Evaluate simple algebraic relations given a particular value of the dependent variable

We should already be familiar with the use of symbols (such as letters) in place of numbers. For instance, we expressed the relationship between a radical and an exponent as follows.

The use of a letter (or any other symbol) allows us to write a general expression that applies to all numbers (or to some specific set of numbers, such as integers, depending on the situation). We wrote the expression above using the letter a; the unspecified nature of a allows us to say that the expression applies to all positive numbers. Without such symbols, we would have to write the expression for every positive number (an impossible task) to show that it applies universally. Our increasing use of symbols sets up our present study of variables and algebraic relations.

Introduction to Variables and Algebraic Relations

A variable is essentially just a symbol that can take on any of a range of values. Thus, a variable is almost identical to the symbols representing unspecified numbers (some differences may exist, but these differences are subtle). Let's say we had a variable x that can be any number, whether positive, negative, or zero.

The expression above could be 1, 5, –2, , –0.476, 108.2, or any other number. As the name indicates, a variable can be "varied" in the sense that it can take on different values. To better understand variables, however, we must also understand algebraic relations.

An algebraic relation is an expression that relates two or more variables. We might view an algebraic relation as a machine (such as a computer) that takes an input value and returns one or more output values according to some formula.

The input to an algebraic relation is a variable that can take on any value from a given set of numbers (such as integers, positive numbers, or negative numbers) without further restrictions. This input variable is called the independent variable, because it does not depend on other variables. The output of the algebraic relation is likewise a variable, but its value is dependent on the input (the independent variable) that is entered in the algebraic relation. Thus, the output is called the dependent variable.

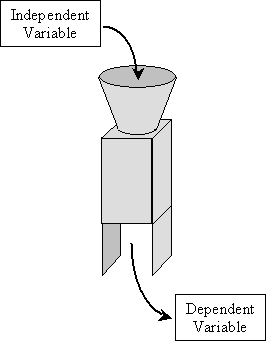
Interested in learning more? Why not take an online Pre-Algebra course?

The next question is how these concepts can be employed mathematically. The algebraic relation machine shown above takes the independent variable, performs some operation or series of operations on it, and then outputs the dependent variable. In other words, the dependent variable is related somehow (perhaps by way of equality, in which case we use the equal sign) to a series of operations on the independent variable. For the purpose of illustration, let's say that the independent variable is x and the dependent variable is y.

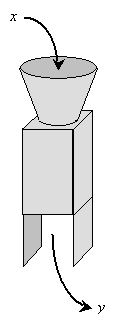
Let's also assume that the algebraic relation machine takes the independent variable input x and produces a dependent variable output y that is equal to some series of operations on x. Mathematically, we can write this as an equality (or equation):

y = (some series of operations on x)

Let's try to illustrate this by way of some simple examples. Let's say the algebraic relation machine simply takes the input (independent) variable, adds 1 to it, and then outputs the (dependent) variable result. Thus, the series of operations in this case is simply addition of 1. The machine illustration and corresponding mathematical expression (equation) for this example are shown below.

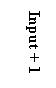
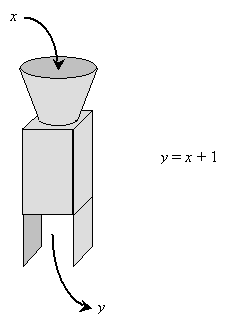
The mathematical expression allows us to easily calculate y (the dependent variable) given a particular value of x (the independent variable). For instance, if x is 1, then y is 2. Likewise, if x is –5, y is –4. The table below shows a few additional results.

–1

0.5

1.5

An even simpler example of an algebraic relation is y = x. To be sure, this case is not all that interesting, but it is nonetheless a legitimate relation. Algebraic relations can also involve multiple operations, as is shown in the example below.

Note that when considering such a relation, we must apply the order of operations to get correct results. In addition, we omit the multiplication symbol for conciseness, but we could also write the relation as shown below. (Be careful to distinguish the independent variable x from the multiplication symbol .)

As a relation gets more complicated, it becomes more difficult to evaluate it by inspection for particular values of the independent variable. In the case of y = x + 1, we can easily see that the values of y is simply one more than the value of x. In more complicated cases, we often must write out the expression and evaluate it on paper. For instance, consider for the case of x = 5. To find y, we simply substitute the given value (5) for the independent variable (x).

Thus, for x = 5, y = 13. We can construct algebraic relations that are as complex as one can imagine. An even more complicated relation is shown below.

Let's determine the value of the dependent variable (y) when the independent variable (x) is 2. Again, we simply substitute 2 for x--this time, we must do so in more than one instance.

To review, then, an algebraic relation takes an input (the independent variable), performs a series of operations, and yields the output (the dependent variable). We can evaluate an algebraic relation for a given value of the independent variable by substituting that value in the expression. When an algebraic relation involves equality (=), then it is called an equation. The following practice problem gives you the opportunity to see different algebraic relations and evaluate them for certain values of the independent variable.

Practice Problem: In each case, identify the dependent and independent variable, then evaluate the expression under the specified conditions.

a. , where t = 2 b. , where d = _{c. , where λ = 6 d. , where g = 4}

Solution: In each case, the dependent variable is the lone variable defined as an expression containing the other (independent) variable. To evaluate the expression to find the value of the dependent variable, simply substitute the given value of the independent variable and evaluate the expression.

a. independent variable = t, dependent variable = z