Key Terms
o Circle
o Equidistant
o Radius
o Diameter
o Circumference
o Pi (π)
Objectives
o Identify some basic parts of a circle, such as the radius and diameter
o Calculate the circumference of a circle
o Calculate the area of a circle
In this article, we will consider a geometric figure that does not involve line segments, but is instead curved: the circle. We will apply what we know about algebra to the study of circles and thereby determine some of the properties of these figures.
Introduction to Circles
Imagine a point P having a specific location; next, imagine all the possible points that are some fixed distance r from point P. A few of these points are illustrated below. If we were to draw all of the (infinite number of) points that are a distance r from P, we would end up with a circle, which is shown below as a solid line.
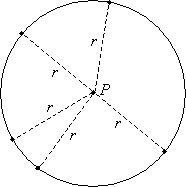
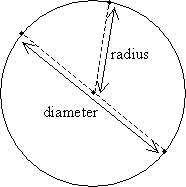
Thus, a circle is simply the set of all points equidistant (that is, all the same distance) from a center point (P in the example above). The distance r from the center of the circle to the circle itself is called the radius; twice the radius (2r) is called the diameter. The radius and diameter are illustrated below.
The Circumference of a Circle
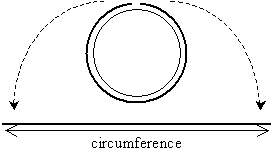
As with triangles and rectangles, we can attempt to derive formulas for the area and "perimeter" of a circle. Unlike triangles, rectangles, and other such figures, the distance around the outside of the circle is called the circumference rather than the perimeter-the concept, however, is essentially the same. Calculating the circumference of a circle is not as easy as calculating the perimeter of a rectangle or triangle, however. Given an object in real life having the shape of a circle, one approach might be to wrap a string exactly once around the object and then straighten the string and measure its length. Such a process is illustrated below.
Obviously, as we increase the diameter (or radius) of a circle, the circle gets bigger, and hence, the circumference of the circle also gets bigger. We are led to think that there is therefore some relationship between the circumference and the diameter. As it turns out, if we measure the circumference and the diameter of any circle, we always find that the circumference is slightly more than three times the diameter. The two example circles below illustrate this point, where D is the diameter and C the circumference of each circle.
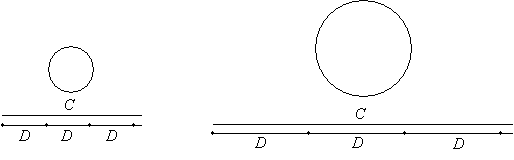
Again, in each case, the circumference is slightly more than three times the diameter of the circle. If we divide the circumference of any circle by its diameter, we end up with a constant number. This constant, which we label with the Greek symbol π (pi), is approximately 3.141593. The exact value of π is unknown, and it is suspected that pi is an irrational number (a non-repeating decimal, which therefore cannot be expressed as a fraction with an integer numerator and integer denominator). Let's write out the relationship mentioned above: the quotient of the circumference (C) divided by the diameter (D) is the constant number π.
We can derive an expression for the circumference in terms of the diameter by multiplying both sides of the expression above by D, thereby isolating C.
![]()
![]()
Because the diameter is twice the radius (in other words, D = 2r), we can substitute 2r for D in the above expression.
![]()
![]()
Thus, we can calculate the circumference of a circle if we know the circle's radius (or, consequently, its diameter). For most calculations that require a decimal answer, estimating π as 3.14 is often sufficient. For instance, if a circle has a radius of 3 meters, then its circumference C is the following.
![]()
![]()
The answer above is exact (even though it is written in terms of the symbol π). If we need an approximate numerical answer, we can estimate π as 3.14. Then,
![]()
![]()
The symbol ≈ simply means "approximately equal to."
Practice Problem: A circle has a radius of 15 inches. What is its circumference?
Solution: Let's start by drawing a diagram of the situation. This approach can be very helpful, especially in situations involving circles, where the radius and diameter can easily be confused.

Because we are given a radius, we must either calculate the circumference (C) using the expression in terms of the radius, or we must convert the radius to a diameter (twice the radius) and use the expression in terms of the diameter. For simplicity, we'll use the former approach.
This result is exact. If we need an approximate decimal result, we can use π ≈ 3.14.
![]()
![]()
The Area of a Circle
Just as calculating the circumference of a circle more complicated than that of a triangle or rectangle, so is calculating the area. Let's try to get an estimate of the area of a circle by drawing a circle inside a square as shown below. The area of the circle is shaded.
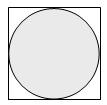
Let's draw a vertical diameter and a horizontal diameter in the circle; we'll label these diameters as having length D. Note by comparison with the square, the square must therefore have sides of length D as well.
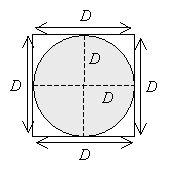
We know that a square (which is a rectangle whose length and width are equal) with sides of length D has the following area Asquare (note that we add a subscript to identify this area as the area of the square-we will add a similar subscript in the case of the area of the circle):
![]()
Because the circle of diameter D obviously has a smaller area than the square with sides of length D, we know that the circle's area must be less than D2. By inspection, we can guess that the area Acircle of the circle is approximately three-fourths that of the square. Thus,
![]()
As it turns out, this guess is close to the actual result. Through some more-complicated mathematics that is beyond the scope tutorial, it can be shown that the area of a circle is exactly the following:
![]()
Notice that the number π once again appears. Let's now compare this exact result with our guess from above. We'll simply do some rearranging of the expression, keeping in mind that the radius (r) is equal to half the diameter (D)-in other words, D = 2r.
![]()
Since D = 2r, then
![]()
![]()
![]()
![]()
Let's substitute this value for r into the expression for the area of the circle; we must make the substitution twice. We can then simplify the expression somewhat.
![]()
![]()
![]()
Since π is approximately 3.14, then
![]()
Thus, our guess was very close to the actual area!
Practice Problem: A circle has a diameter of 6 centimeters. What is its area?
Solution: Note carefully that the diameter is given, not the radius. Thus, if we are to use the expression for the area in terms of the radius, we must convert the diameter to a radius (simply by dividing the diameter in half).
![]()
We can now calculate the area using the following formula.
![]()
![]()
![]()
Again, this answer of 9 square centimeters is exact. But,
![]()
![]()
This is an approximate result, but would be sufficient in many contexts.
Practice Problem: A circle has a circumference of 8π feet. What is its area?
Solution: We learned that the circumference is closely related to the radius (and diameter). Thus, using this known value of the circumference, we can calculate the radius and use it to find the area. First, let's solve the expression for the circumference to get the radius.
![]()
![]()
We want to isolate r; we can use the same approach as we used when solving linear equations.
![]()
![]()
![]()
![]()
Now that we know the radius of the circle, we can calculate its area.
![]()
![]()
![]()
Or,
![]()
![]()