Introduction
In this article, we are going to review the vector. Vectors--unlike simple numbers (scalars) that have only a magnitude--have both a magnitude (length) and direction. We will explore how to represent vector quantities, as well as how to add and subtract them.
Key Terms
Objectives
Individual numbers--that is, values that have only (positive or negative) magnitude--are called scalars. The numbers 0, –3, π, i, 1.3, e, and so on are all examples of scalars. Another type of value that is often useful in math is the vector. A vector is a quantity that has both magnitude and direction. In this article, we will consider some of the mathematical characteristics of vectors. Vectors have extensive applications in, for example, physics.
Introduction to Vectors
To understand the difference between a scalar and a vector, it helps to think of physical examples. Consider temperature, for instance. You can use a thermometer to measure the air temperature at different locations. In each case, you get some number (and a unit)--say, 65°F. This is a magnitude, but it has no direction associated with it; it is thus a scalar quantity. Now, consider measurements of the wind at these same locations. When you measure the wind, you would likely measure both the speed and the direction. Thus, your wind measurements constitute a vector. We might express this vector as an arrow pointed in the direction of the wind, with the length of the arrow being proportional to the wind speed. Below is an illustration of two wind measurements taken at different points; the arrows represent the vectors associated with these measurements.

Vectors have a magnitude and direction, but they do not have an assigned location per se. That is, as long as the direction and length of the "arrow" is maintained, we can move it anywhere we want without changing it. This is an important characteristic that will let us work extensively with vectors.
A Representation of Vectors
Our first task is to find a way to cleanly and consistently represent vectors. Graphically, this is simple: because we can move a vector anywhere we want, let's always position the "tail" of the vector at the origin of the coordinate plane. (Note that the "head" and "tail" of a vector are defined as shown below.)
![]()
![]()
Now, with the tail of the vector placed at the origin (remember, we can move the vector anywhere as long as we maintain its direction and length), we can quantify it as the coordinates of the head. An example is shown below for vector v. (Note that to differentiate symbols representing vectors from those representing scalars, we use boldface. Another common method is to use a little arrow above the symbol: for instance, vector ![]() .)
.)
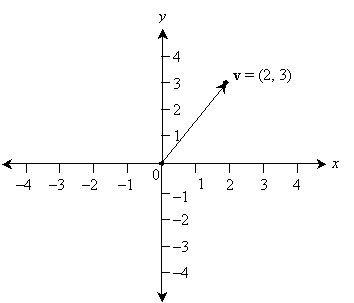
Thus, the vector v is simply the coordinates of the point at (2, 3). Note that all of the vectors shown below are equal to (2, 3)--our convention is that the vector is described by the coordinates of the point at its head only when its tail is positioned at the origin.
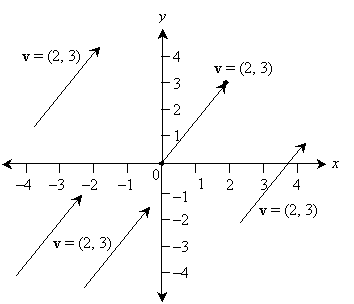
Although we have shown the vector only in two dimensions, this approach can be generalized to any number of dimensions. For instance, in three dimensions, a vector will have the form (x, y, z). All of the properties of two-dimensional vectors can be easily extended to three dimensions.
But how do we go about "moving" the vector, from a numerical perspective? For instance, say a vector v has its head at (3, 2) and its tail at (1, 4).
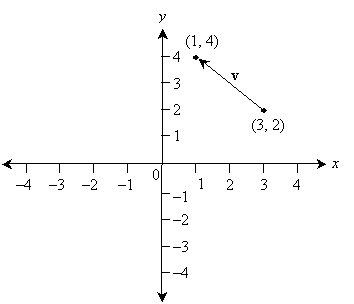
The answer lies in translating (or moving) both the head and the tail over an equivalent distance and in the same direction. This translation should result in the tail of the vector moving to the origin--a simple process that involves subtracting each tail coordinate from itself. In the above example, the result is (3 – 3, 2 – 2) = (0, 0). To translate the head, likewise subtract the tail coordinates from the head coordinates--this satisfies our criterion that the translation have a fixed distance and direction. Thus, the head should be moved as follows: (1 – 3, 4 – 2) = (–2, 2). Thus, in general, to find the value of an arbitrarily placed vector, subtract the coordinates of the tail from the coordinates of the head. This process is illustrated below.
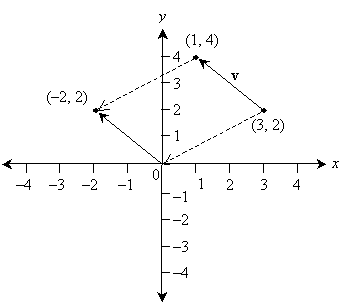
Note that the vector (0, 0), sometimes called the zero vector, has a length of 0 but no defined direction. (That is, no matter what direction you pick, the zero vector is the same.)
Practice Problem: Determine the value of each vector shown in the graph below.
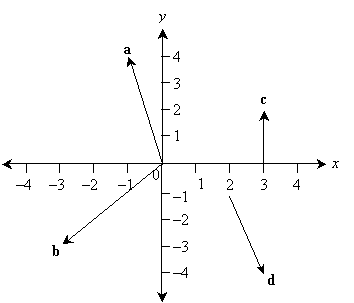
Solution: In each case, you can find the coordinate expression for the vector by subtracting the tail coordinates from the corresponding head coordinates. This works even when the tail is at the origin, which has coordinates (0, 0). But if the tail is at the origin, the vector is also simply equal to the coordinates of the head. If it helps you, redraw the vectors with tails positioned at the origin.
a = (–1, 4)
b = (–3, –3)
c = (3 – 3, 2 – 0) = (0, 2)
d = (3 – 2, –4 – [–1]) = (1, –3)
Adding and Subtracting Vectors
As with scalars, we can add and subtract vectors. The process is similar, but with one or two caveats. To add or subtract two vectors a and b, add or subtract corresponding coordinates of the vector. That is, where a and b are defined as follows, here are the rules for addition and subtraction.
![]()
![]()
![]()
Note that as with scalars, addition of vectors is commutative, but subtraction is not. Graphically, we add two vectors a and b by positioning the tail of b at the head of a and then creating a new vector starting from the tail of a and ending at the head of b. The coordinates of this new vector are determined in the same way as before: by positioning its tail at the origin. This process is illustrated below for vectors a = (4, 1) and b = (-1, 2).
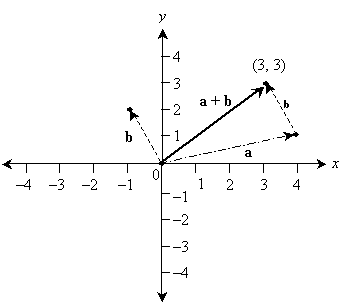
Note that
![]()
Subtracting vectors follows basically the same procedure as addition, except the vector being subtracted is "reversed" in direction. Consider the same vectors a and b as above, except we'll calculate a – b. (Note that this is the same as ![]() , where –b has the same length as b but is opposite in direction.)
, where –b has the same length as b but is opposite in direction.)
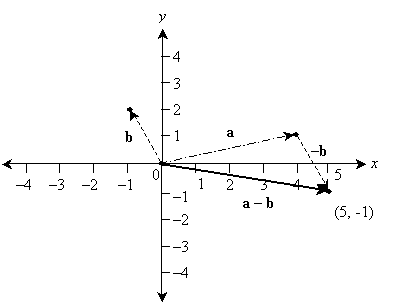
Here,
![]()
Practice Problem: Perform the following vector operations.
a. (3, 2) - (4, 5) b. (-1, 5) + (10, -6) c. (-1, 0) - (0, 0)
Solution: In each case, add or subtract corresponding coordinates to find the result. One helpful way to check your answer is to draw the vectors on the graph, showing the addition or subtraction and comparing your results.
a. (-1, -3) b. (9, -1) c. (-1, 0)