Objectives

  

 

Introduction to Sequences

 

Consider the natural numbers, a portion of which are shown below.

 

1, 2, 3, 4, 5, 6, ...

 

This ordered group of numbers is an example of a sequence. More broadly, we can identify an arbitrary sequence using indexed variables:

 

 

The variables a_i (where i is the index) are called terms of the sequence. Although this construct doesn't look much like a function, we can nevertheless define it as such: a sequence is a function with a domain consisting of the positive integers (or the positive integers plus 0, if 0 is used as the first index value). The range of this function is the values of all terms in the sequence. Coincidentally in the case of the natural numbers, the domain and range are identical (assuming the first index value is 1--an assumption that we will stick with here).

 

As a more concise representation, we can express the general sequence above as {a_n}. Also, we can reference the nth term of the sequence as just a_n. Thus, for instance, given the sequence 1, 2, 3, 4, 5, 6,..., which we might call {a_n}, the nth term is simply n. (The sixth term, a₆, is 6, for example.)

 

In addition, the terms of a sequence {a_n} may be related to an algebraic expression. Consider the following example:

 

 

 

 

 

Thus,

 

 

 

 

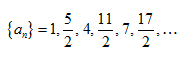
Practice Problem: Write the first five terms in the sequence .

 

 

Solution: Remember that we are assuming the index n starts at 1. Thus, the first term corresponds to n = 1, the second to n = 2, and so on. The terms are then

 

 

 

 

 

 

 

 

Introduction to Series

 

 

 

Series are similar to sequences, except they add terms instead of listing them as separate elements. A series has the following form.

 

 

 

 

Again, we will assume that the first index of the series is 1 unless otherwise indicated (0 is the other common first index). We can express a series more succinctly using sum notation:

 

 

 

 

 

 

Note that in general, a series is infinite. This notation can also have the form below:

 

 

 

 

 

 

We can also consider a portion of the series: S_n, which is defined below, is called the nth partial sum of the series.

 

 

 

 

 

 

As with sequences, series can be use algebraic expressions. Consider the example below, which is the sum of all (positive) odd numbers.

 

 

 

 

 

 

 

Practice Problem: Using sum (∑) notation, write an expression for the sum of every other even number, starting with 2.

 

 

 

Solution: It helps to first write out the first few terms of this series.

 

 

 

2 + 6 + 10 + 14 + 18 + ...

 

 

 

Note that the increment is 4 in each case. So, let's write the expression for the series as follows. (This expression uses an initial index of 1, but you can also write an expression with an initial index of 0.)

 

 

 

 

 

 

Check the result by calculating the first several terms of the series.

 

 

 

 

 

Convergence of Sequences and Series

 

 

 

One of the most important questions we can ask about a sequence or series is whether it converges. In the case of a sequence , if the terms get arbitrarily close to a certain fixed value as n approaches ∞, then the sequence converges. Otherwise, the sequence diverges. But this sounds very close to our definition of a limit. Although we will not cover the precise mathematical proof of convergence for a sequence, we can intuitively visualize what convergence looks like. Consider the following sequence .

 

 

 

 

 

 

Let's graph the points of this sequence.

 

 

 

 

 

 

 

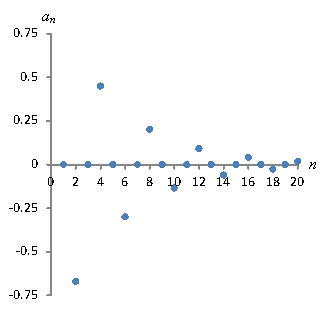
Although the terms "oscillate" around 0, obviously they approach 0 as n approaches infinity. Try a very large value of n and plug it into the expression; you'll find the result is very close to zero. This sequence converges. Furthermore, the limit of this sequence is 0, since

 

 

 

 

 

 

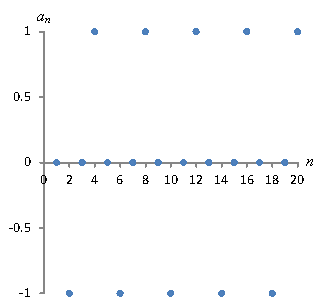
On the other hand, the sequence diverges because it doesn't approach any particular value as n approaches ∞.

 

 

 

 

 

 

In a similar manner, a series converges if it is equal to a finite number. Otherwise, it diverges. Thus, a convergent series has the following characteristic, where k is a real number:

 

 

 

 

 

 

In some cases, we can see that a series obviously diverges. For instance,

 

 

 

 

In other words, the series adds constantly increasing values, so the sum grows without limit. As it turns out, if the sequence {S_n} of nth partial sums for a series diverges, then so does the series. This is clear in the above case: this sequence is

 

S_n = 1, 3, 6, 10, 15, 21, 28,...

 

Since this sequence obviously diverges, so does the series.

 

To close, let's consider a couple other series.

 

 

 

 

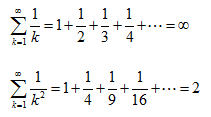
Interestingly, then, note that some series--even though they have an infinite number of terms--still converge. Here again, we will not get into the mathematical machinery for proving convergence or divergence of a series. It is important to simply note that divergence or convergence is an important property of both sequences and series--one that will come into play heavily in calculus (particularly integral calculus).

 

 

 

 

 

Practice Problem: Determine if the series converges.

 

 

 

Solution: Look at the terms in the series:

 

 

 

 

 

 

Because the terms are increasing in size as n approaches ∞, the series does not converge (i.e., it diverges). You can also calculate the sequence of nth partial sums, which appears to diverge also, meaning the series diverges.