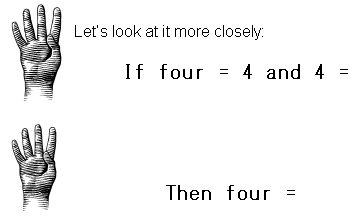| Number line and 1 - to -1 correspondence |
Even before you could count on your fingers, you counted objects. For example, if you had six little cars you played with every day, you knew when one was missing. How did you know? You knew what each one looked like: you knew there was a green one, a blue one, a red one, a red and yellow one, etc. When the black one with flames on the side was missing, you may not have known that there were only five cars, but you certainly knew that one was gone! This is a very basic type of one-to-one correspondence – one car corresponds to one color or color combination.
When you started counting on your fingers, each finger corresponded to a number. You always said "one" when you put your index finger up or pointed to it (for some people "one" is the thumb). "Two" was the next finger, then "three" and so forth until you got to the last finger which was "ten." Each finger corresponded to the same one and only one number each time. This is known as one-to-one correspondence.
In the same way, the points (dots) on a number line correspond to one number:

For the number line above, "1" corresponds or is related to the red point, "2" is related to the green point, "3" is related to the blue point, and so forth. When we move to the right on the number line, we increase in numbers and when we move to the left, we decrease. This is generally the way a number line works.
| Numbers |
On the number line above, we can see three types of numbers, or integers: negative numbers, zero, and positive numbers. The negative numbers are to the left of zero, so they are less than zero. The positive numbers are to the right of zero, so they are greater than zero. Zero, the dividing point, is neither positive nor negative.
Counting numbers, also known as natural numbers, start with the number one and go to the right so that they are all positive. The even numbers start with 2 and skip every other number such as 2, 4, 6, 8, 10, 12, . . . They can be divided into two groups with the same number in each group. The odd numbers start with 1 and skip every other number such as 1, 3, 5, 7, 9, 11, . . . They cannot be divided into two equal groups. One group will always have one more object in it than the other. Whole numbers start with the zero and go to the right, so they are zero and the positive numbers. (You can remember the difference because "whole" has an "O" in it, so there is a "0" with whole numbers.)
Between any two numbers are many other numbers such as 1/2, 4/7, 0.764, √16. These numbers are known as nonintegral rational numbers. When they are included in the number system, instead of integers, we now have the rational numbers.
| Numerals, Digits and Place Value |
From this point on, the word ‘number' will mean one of the real numbers. Technically, we can distinguish between "number" and "numeral" as follows. A numeral is the written representation of a number: when you write 0, 1, 2, and so on, technically you are writing numerals. A number is the value represented by the numeral. Although these terms, therefore, actually have different meanings, we will often use them interchangeably, unless otherwise noted.
Single digit numerals are the numbers 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. Ten is the first double digit (2-digit) number, 100 is the first triple digit (3-digit) number, and 1,000 is the first 4-digit number.
Note: A digit is sometimes called a figure. For example, a five-figure salary would be a salary of $10,000 to $99,999.
It is important to look at digits when we learn about place value since place value is the value represented by a digit with respect to its placement in the numeral. Let's consider 538. As five hundred thirty eight, we understand the ‘5' means five one-hundreds or ‘500,' the ‘3' means three tens or '30,' and the ‘8' means eight ones. Likewise, 4279 is really ‘4 thousands,' ‘2 hundreds,' 7 tens,', and ‘9 ones.'
4279 = 4,000
200
70
____9
4,279
| Equivalence |

A number sentence is a way of showing that two expressions have a relationship. In this case, the two are equivalent. In the example, one expression is "3 cats" and the other is the picture of the three cats. An "equals" sign (=) is used between the two expressions to mean ‘is equivalent to.'
A number sentence could have a different sign to express another relationship between the expressions:
≠ ‘is not equal to'
< ‘is less than'
> ‘is greater than'
| Variables |
A symbol that holds a place for a numeral in a number sentence is called a placeholder, or variable. Often, the variable represents an unknown quantity which needs to be calculated using the other parts of the number sentence.
We could say that 26 is equivalent to 2 tens and 6 ones.
Or, we could say that 2 tens and 6 ones is equivalent to □
or 2 tens and 6 ones = □.
The box □ becomes a placeholder or variable. Because it is cumbersome to stop and draw a box, we often use a letter for a variable such as:
2 tens and 6 ones = x
The replacement for the box or the letter x that makes this number sentence true is '26.'
A number sentence that contains a variable is called an open sentence. One that does not contain a variable, whether it is an equality or inequality, is either true or false.
For example, 2 tens and 6 ones = 32 would be a false number sentence.
A number sentence in which the expression on the left of the equals sign is equivalent to the expression to the right of the equals sign is called an equality or an equation.
There are three equations which are true for all numbers. Because they are like ‘laws of numbers,' we refer to them as axioms. You will also see them referred to as properties of equality or properties of numbers.
| Reflexive axiom |
The reflexive axiom or reflexive property tells us that any quantity is equal to itself.
a = a
In other words, 5 = 5 and 4,579 = 4,579.
| Symmetric axiom |
The symmetric axiom or symmetric property says that if one quantity is equivalent to another quantity, you can switch which side of the equals sign they are on.
If a = b, then b = a.
For example, if 32 = 3 tens and 2 ones, then 3 tens and 2 ones = 32. The ‘32' is the ‘a' and the ‘3 tens and 2 ones' is the ‘b.'
| Transitive axiom |
The transitive axiom or transitive property says that if two quantities are equal to a third quantity, then they are equal to each other.
If a = b and b = c, then a = c.