Math Skills: How to Do Subtraction

What Subtraction Is

Subtraction is taking away one or more items from a group of items. In other words, if there are 4 boys and 2 girls going to class, but the 2 girls decide to go to lunch, how many young people are going to class?

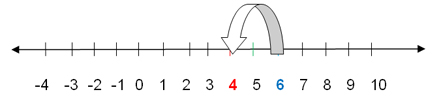
Our first method of figuring out how many is to physically count them.

When we plot our counting like this, it looks similar to the number line for subtraction.

Movement on a Number Line

On the number line, we locate the number 6 (for the 6 boys and girls) and then we move to the left 2 ticks to subtract the 2 girls. The number on which we land is 4 which is the same number we got when we counted.

In this way, we see subtraction as the opposite or inverse of addition.

If 2 + 3 = 5, then we know that 5 – 3 = 2 and 5 – 2 = 3.

Grouping of objects

If we have a group of objects and some of those objects are no longer with the group, we may need to know how many objects are now in the group.

By counting the trees that are left, we know that 5 are left. Therefore, 8 – 3 = 5.

This works fine for smaller numbers, but gets complicated as our numbers get larger. Therefore, we need some other ways of looking at subtraction.

Terms - Minus, Subtrahend, Minuend, Difference, Less, Take Away

Just as we used a ‘+' sign for addition, we now use a ‘-‘ sign, called a minus sign, for subtraction. We refer to the number being subtracted as the subtrahend and the number it is subtracted from as the minuend. The answer is the difference.

9 minuend
- 5 subtrahend

______

4 difference

Want to learn more? Take an online course in Basic Math.

We can say "the subtrahend from the minuend is the difference." For example, 5 from 9 is 4. Or, we can say "the minuend minus the subtrahend is the difference" as in 9 minus 5 is 4. Other ways of saying the same thing are 5 less than 9 is 4 and 9 take away 5 is 4.

Unlike addition where we can add many numbers at a time, in subtraction we can only subtract one number from one other number. If there are more numbers to be subtracted, they must be done one at a time.

Subtraction Facts

Subtracting becomes easier and quicker if we memorize some subtraction facts. The addition facts are one through ten in one direction (left to right) and one through twenty in the other direction (top to bottom). By using the answers within the table, we can subtract the number along the top (or left) and the answer is the number along the left (or the top).

To subtract 8 from 15, find 8 along the top and follow it down to 15, then go straight left along the row to 7 which is the answer. By memorizing the subtraction facts, your life will become much easier. You will be able to quickly subtract a group of numbers simply by looking at them.

Additive Identity Element

An identity element is a specific number that when put with any other number in a specific way gives the original number. Zero is the additive identity element. It is also a subtractive identity element. Zero plus any number is the original number; an original number minus zero is the original number.

a + 0 = a
6 + 0 = 6 and 13 + 0 = 13
a – 0 = a
6 – 0 = 6 and 13 – 0 = 13

Simple Subtraction

Knowing the subtraction facts and lining up digits according to their place values will help you with subtraction problems. Always start with the farthest right column – in this case the ones.

27
-6

_______
21

Seven minus six is one. And two minus nothing is two. However, you should really look at it as 7 ones minus 6 ones is 1 one and 2 tens minus no tens is 2 tens. Therefore, the answer is 2 tens and 1 one or twenty-one.

369
-252

_______
117

In this problem 9 ones minus 2 ones is 7 ones, 6 tens minus 5 tens is 1 ten, and 3 hundreds minus 2 hundreds is 1 hundred. The answer is 117.

Subtraction Necessitating Borrowing

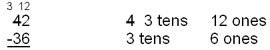
Sometimes a digit in the subtrahend will be larger than the corresponding digit above it in the minuend. When that happens, you will need to borrow from the digit to the left. For example:

You cannot take 6 ones from 2 ones. So you have to borrow 1 ten from the 4 tens, so now the 2 ones is 1 ten and 2 ones, or 12 ones.

Now you can subtract 6 ones from 12 ones and get 6 ones. And when you subtract 3 tens from 3 tens, you get nothing. So the answer is 6.

Let's try a larger number with a bit more borrowing:

In this problem, you cannot subtract 8 ones from 4 ones, so you borrow 1 ten from the 5 tens. This gives you 14 ones minus 8 ones. So your answer contains 6 ones.

Now you cannot subtract 6 tens from 4 tens, so you must borrow 1 hundred which is 10 tens to add to the 6 tens, giving you 14 tens. When you subtract the 6 tens, you get 8 tens:

In order to subtract the 7 hundreds from the 1 hundred, you must borrow 1 thousand from the 6 thousands, giving you 11 hundred from which to subtract 7 hundred.