?
Thus far, we've introduced power supplies, resistors, and switches, and we've studied the meaning of voltage, current, resistance, and power dissipation in circuits. This article considers another type of electronic component: the capacitor.
Key Terms
o Capacitor
o Capacitance
o Farad
Objectives
o Recognize the function of a capacitor
o Analyze simple circuits containing capacitors
Resistors are important electronic components, but there's much more to many complex electronic circuits. Resistor networks are fairly "static," meaning their parameters don't change much over time. That's fine in the case of, say, a light bulb--generally, you want a steady light source rather than flickering or flashing. But what if we want to do some more interesting things, like, for instance, create a voltage drop that decreases or increases over time? We need something more than just resistors. In this article, we'll discuss one such component: the capacitor.
What Is a Capacitor?
Charge can move in a conductor, and it is moved by the electric force. Generally, wires are electrically neutral, but they can conduct charge, and charge can also build up in portions of the material in response to electric forces. Imagine the scenario below, where we have our usual power (voltage) source. Each terminal is connected to a metal plate, but these two plates are separated by an insulator (such as air), meaning no charge can move between them. Also, we'll add a switch that starts in the "open" position.
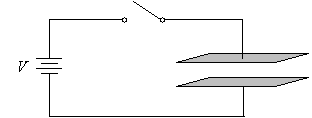
When the switch is open, nothing happens-the bottom metal plate is at "ground," and the top metal plate is disconnected from any voltage source. (We'll assume it is at ground" as well.) Thus, no electric forces exist between the plates. Now, let's close the switch and see what happens.
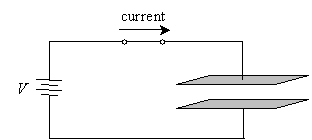
Initially, as the current just begins to flow in the circuit, the two plates have no voltage difference across them. But positive charge moves from the power supply's positive terminal toward the upper plate and begins accumulating (the lower plate is at ground, and the positive charge is pulled toward it by the electric force). Note that current can't flow between these plates because they are separated. As positive charge accumulates in the upper plate, positive charge is pushed away from the lower plate, leaving it with an equivalent negative charge.
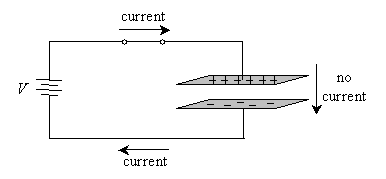
Charge will accumulate until the voltage drop between the two plates is equivalent to the supply voltage, V. Note that the existence of an electric force between the plates (and thus an electric potential difference) is clearly seen because one plate is positively charged and the other is negatively charged. In essence, these plates are like a power supply that is "charged" or "energized" by the battery (or other supply) in the circuit. In other words, these plates are able to store electrical energy by accumulating charge. Such a device involving conducting plates--whatever their shape--is called a capacitor. We'll use the following intuitive circuit symbol for a capacitor.
As you might guess, larger plates leave more room for charge to accumulate. Furthermore, the closer the plates, the stronger the force between accumulating charge. The ability of a capacitor to hold charge is called its capacitance, which we'll denote as C. (The SI unit of capacitance is the farad --we won't deal with this unit much, though. Nevertheless, one farad is equal to one coulomb per volt, which is fairly intuitive if you think about it!) If the capacitor can hold more charge for a given voltage drop across it, then its capacitance is higher.
Practice Problem: A capacitor has a capacitance of 1 farad. If the voltage drop across it is 10 volts, how many coulombs of charge can it hold?
Solution: Use the definition of a farad: it is how much charge a capacitor can hold as measured in coulombs per volt of voltage drop. Thus, if the capacitor has a voltage drop of 10V, it will hold 10 coulombs of charge. (Multiply the voltage drop by the charge "capacity"--this should be the same as the capacitance in farads. In other words, use the relation Q = CV, where Q is the charge stored in the capacitor, C is the capacitance, and V is the voltage.)
What Can Capacitors Do?
It may not be immediately obvious to you how capacitors can be used. But for now, let's look at the circuit below to see what a capacitor can do.
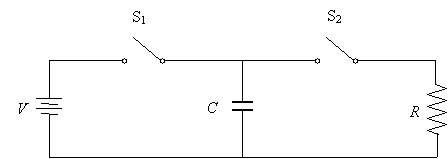
First, close switch S1 to charge the capacitor; because S2 remains open, no voltage drop exists across the resistor, so it doesn't participate in the functioning of the circuit.
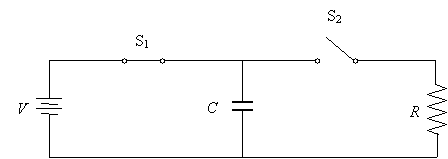
As we discussed above, the capacitor will "charge" until it reaches voltage V. (The time it takes this process to occur depends on a number of factors--if the wires are truly perfect conductors, the process is instantaneous, but if the wire has some resistance, as it does in reality, then this process takes some finite amount of time.) Once the capacitor is charged, we open switch S1; The upper plate maintains its charge (because it is not connected to ground), so the voltage across C remains V volts.
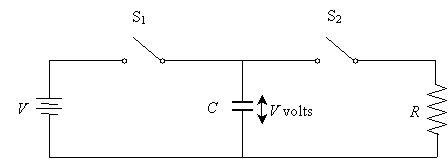
Now, close switch S2. The positive charge on the top plate of the capacitor now has a route to ground--through resistor R. Following the circuit-analysis principles, we know that (initially) the voltage drop across the resistor is V.
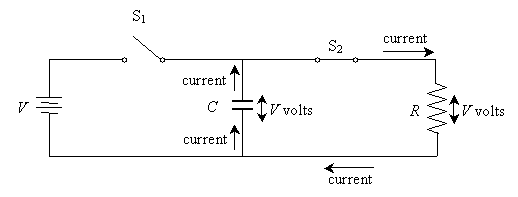
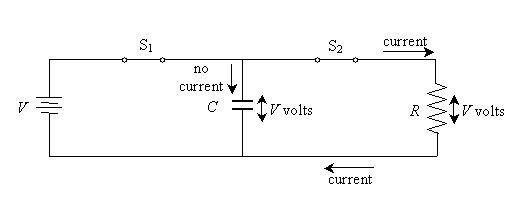
But as the excess charge in the top plate of the capacitor flows to ground, the capacitor loses its stored energy, meaning its voltage decreases. Thus, according to Ohm's law, the current decreases as well. This process continues until the charge on the capacitor is depleted; at this point, the circuit is "dead" (meaning simply that there is no more voltage across or current through R and C). (Incidentally, the positive charge in this case may best be seen as traveling to the lower plate of the capacitor, where it "neutralizes" the negative current that accumulated when the capacitor was charged.)
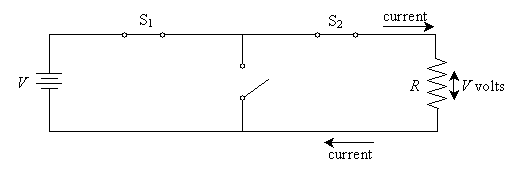
At this point, the capacitor must be recharged to repeat the process. If both switches are closed simultaneously in this circuit, then the capacitor is likewise charged, but once it reaches its maximum capacity, the only current flowing is that through the resistor R. This current can be found using Ohm's law.
Thus, when fully charged in this circuit, the capacitor is effectively the same as an open switch!
This article has only briefly introduced the capacitor, and it has done so with minimal mathematics. To truly understand what is happening with capacitors, we would require complex math and more-sophisticated electrical theory. But, as you can see from the brief discussion above, capacitors are electronic components that can store electrical energy by storing charge. This function is important in, for instance, radio communication circuits, just to name one example!